| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 정부24 개요
- 정부24
- 토론 태도
- 정의
- 조던 피터슨
- 논증
- 책
- 독서 토론
- 정책정보
- 위계
- 독서
- 토론 대첩
- 정책 정보
- 타당한 논증
- 토론 문화
- 정책 자료
- 정책 정보 포탈
- 논제
- 이념 정당
- 포스트 모더니즘
- 정부24의 주요메뉴
- 토론 기획
- 수권 정당
- 포스트모더니즘
- 발제 자료
- 토론 정의
- 정책
- 발제
- 논제 자료
- 토론
- Today
- Total
토론 기획하는 남자, 토기남
측도 본문
이번 글은 측도라는 단어가 전혀 다른 학문에 사용되고 있다는 점을 짚기 위해 썼다.
1,2,3 문단은 수학에서의 측도(measure)를 다룰 것이고
4 문단은 사회과학에서의 측도(measurement level)을 다룬다.
1. 수학에서의 측도(measure)
어떤 집합의 크기를 재는 함수를 측도라고 말한다.
측도가 부여된 집합을 측도 공간(measure space)이라고 한다.
이와 같이 측도와 측도 공간을 연구하는 수학 분야를 측도론(measure theory)이라고 한다.

예를 들어, 물 한 컵이 있다고 하자.
물이 '얼마나' 들어있는가를 어떻게 설명할 수 있을까?
물이 담겨있는 높이를 재서 알려주거나(m),
부피를 계산(cc),
혹은 물 분자를 일일이 세서 알려줄 수 있을 것이다(mol).
이처럼 물이 담겨있는 컵과 그 안의 물에 크기 개념을 부여하는 작업을
집합과 원소의 개념으로 확장했을 때의 개념을 측도(measure)라고 한다.
길이, 질량, 개수, 부피, 확률, 온도 등등 단위를 사용하는 온갖것들이 측도가 될 수 있다.
이를 직관적으로 표현하면 아래와 같다.
측도 : 집합에 '크기'라는 개념을 부여하기 위해 추상적으로 정립한 것
2. 선택 공리(Axiom of Choice)
측도 개념은 'ZFC 공리계'에서 'C'에 해당되는 선택공리와 밀접한 관계를 맺고 있다.
*공리계 : 주어진 이론 체계 안에서 증명없이 참인 것으로 받아들이는 명제들이 구성하는 체계
*ZFC 공리계 : 표준 수학 공리계
선택공리

위 수식을 다르게 표현하자면,
공집합을 포함하지 않는 모든 집합족은 선택 함수를 갖는다.
즉, 모든 무한 집합은 셀 수 있는 부분집합을 가진다.
측도는 다음의 조건을 만족해야 한다.

다르게 표현하자면,
(1) 잴 수 있는 집합에 대해서
(2) 원소가 없는 공집합은 크기가 0,
(3) 겹치는 부분이 없는 셀 수 있는 집합들의 합집합은 측도의 합과 같아야 한다
는 의미인데,
선택 공리와 측도의 조건을 잘 비교해보면
우리는 측정하길 원하는 대상들만 골라 선택하므로,
측도를 재길 원하는 집합들만 깔끔하게 모아놓을 수 있는 특정한 조건을 만족하면
그 위에서 측도를 정의할 수 있다는 것을 알 수 있다.
굳이 모든 부분집합들을 잡을 필요는 없는 것이다.
3. 연속성의 수량화
그래서 뭐?
아니, 애초에 왜 수학자들은 굳이 어려운 측도라는 개념을 쓰는 것일까?
이는 역사적 배경과 관련이 있다.
19세기 해석학의 발전으로, 기존의 길이나 넓이가 불충분하게 느껴지기 시작했다.
대표적으로 무한 집합의 크기에 대한 의문이있다.
예를 들어, '0과 1사이의 유리수로 된 집합의 길이'는 얼마인가?
0과 1사이의 유리수는 무한하며, 어떤 순서로 세야할지 감도 잡히지 않는다.
고전적 크기 개념으로는 해결되기 어려운 질문이었던 것이다.
그런데 위의 측도의 조건을 생각해보면 손쉽게 구할 수 있게 되는 것이다.
선택 공리에 따르면 무한한 집합이어도 셀 수 있다.
따라서 다음과 같이 표현할 수 있다
{x|x는 0과 1사이의 유리수}= {1/2, 1/3, 2/3, 1/4, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6 .... }
길이 측도로 유명한, 르벡측도(Lebesgue measure)에서
점에 해당되는 숫자하나의 길이는 0이다.
따라서 각각의 르벡측도인 0을 무한번 더한 것이 위 집합의 길이가 된다.
따라서 답은 0이다
4. 사회과학에서의 측도 : 측정 수준(measurement level)
측도(measure)와 비슷한 단어가 있는데,
바로 사회과학에서 이야기하는 '측정 수준(measurement level)'이다.
측정 수준을 분류하는 이유는 분석 수준이 달라지기 때문인데,

위 질문의 통계자료를 다룬다고 생각해보자,
명목 수준에 해당되는 데이터이므로,
단순히, 어느 지역에 거주하는 사람이 많은지 이야기하는 정도의 분석만 가능하다.
예를 들어, '2번에 해당되는 경기도 사람들이 가장 많습니다'와 같은 답변을 말한다.

반면, 등간 수준에 해당되는 위 질문에서는 보다 다양한 분석이 다양하다.
평균을 내어, '저희 사이트의 평균 연령은 24.3세 입니다'라고 이야기 할 수 있다.
이해를 돕기 위해《조사방법의 이해와 SPSS 활용(한승준)》 에서 표를 인용했으니, 참고바란다
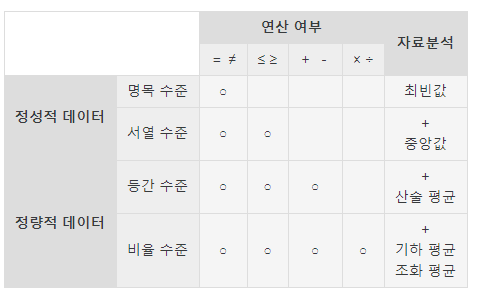
이처럼, 측정 수준에 따라 사용할 수 있는 대푯값들이 늘거나 줄 수 있다는 것을 알 수 있다.
한편, '측정 수준'을 '측도'라고 표현하기도 한다는 것을 주의하자
실제로 SPSS에서 measurement level이 "측도" 라고 번역되어 있는 것을 확인할 수 있다.
허나 이는 뜻과 목적이 다른 동음이의어이다.
*SPSS : 통계 소프트웨어 중 하나
'토론 기획을 위한 정리글' 카테고리의 다른 글
| 정당 (0) | 2020.04.28 |
|---|---|
| 수권정당과 이념정당 (0) | 2020.04.25 |
| 과학 (2) (0) | 2020.04.20 |
| 과학 (1) (0) | 2020.04.20 |
| 수학 (0) | 2020.04.20 |



